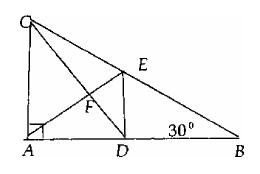
Perhatikan gambar di bawah ini. Jika CE = EB, AD = DB, besar sudut ABC 30°, dan panjang CA = 4 cm, maka panjang CF adalah .......

a. 4/3 √28

b. 1/3 √28

c. 2/3 √7

d. 4/3 √7

e. 1/3 √7

Jawaban

Persoalan ini bisa diselesaikan dengan prinsip segitiga sebangun

Perhatikan segitiga ABC dan segitiga DBE, karena CE = EB, AD = DB, besar sudut ABC = sudut DEB =30°, maka segitiga ABC dan segitiga DBE sebangun.

Oleh karenanya didapatkan hubungan perbandingan panjang sisi segitiga sebangun sebagai berikut,

> DE/CA = DB/AB = 1/2

> DE = 1/2 CA = 1/2 x 4 cm = 2 cm

dan karena segitiga ABC dan segitiga DBE sebangun, didapatkan juga bahwa AC sejajar dengan DE, sehingga segitiga AFC sebangun dengan segitiga DFE.

Oleh karenanya didapatkan hubungan perbandingan panjang sisi segitiga sebangun sebagai berikut,

> FD/CF = DE/CA = 2/4 = 1/2

> FD = 1/2 CF

> CD = CF + FD = CF + 1/2 CF = 3/2 CF

> CF = 2/3 CD   (1)

Untuk mendapatkan nilai CD, kita memerlukan nilai CF terlebih dahulu yang bisa didapatkan dengan menghitung dengan rumus phytagoras dari segitiga CAD dengan terlebih dahulu menghitung nilai AB

> AB = AC / tan30° = 4/(1/3√3) = 4√3

> AD = 1/2 AB = 2√3

> CD = √[AD^2 + AC^2] = √[12 + 16]

> CD = √28 = 2√7 (2)

Substitusikan nilai CD pada persamaan (2) ke dalam persamaan (1)

> CF = 2/3 CD = 2/3 x 2√7 = 4/3 √7